2 Law Firm Analysis

2.1 Introduction

In this chapter, we act as data scientists working for a law firm that specializes in fighting parking and camera tickets. The goal of this analysis is to uncover patterns in NYC violation data in order to better understand trends across different aspects of ticketing and inform the firm’s marketing strategy. Using the Open Parking and Camera Violations Data from NYC Open Data, we explore whether payment amounts differ by issuing agency, plate state, and county. To answer these questions, we use data cleaning, visualization with ggplot2, descriptive statistics, and one-way ANOVA to assess whether observed differences are statistically meaningful.

In this analysis we explore three questions:

1. Do certain agencies issue higher payments?

2. Do drivers from different states (NY, NJ, CT) pay more?

3. Do certain counties tend to have higher payment amounts?

2.2 Required Packages

First, we load the packages used in this report.

library(tidyverse)
library(httr)
library(jsonlite)
library(supernova)
library(AICcmodavg)
library(mosaic)

2.3 Data Ingestion via API

Next, we pull the Open Parking and Camera Violations data directly from NYC Open Data using httr::GET() and the endpoint below.

endpoint<-"https://data.cityofnewyork.us/resource/nc67-uf89.json"

resp <- httr::GET(endpoint, query = list(
  "$limit" = 99999,
  "$order" = "issue_date DESC"
))

camera <- jsonlite::fromJSON(httr::content(resp, as = "text"), flatten = TRUE)

2.4 Cleaning Data

Now that the dataset was successfully loaded, we began the data cleaning process.

camera<- camera %>% 
  mutate(payment_amount = as.numeric(payment_amount))

We first converted the payment_amount variable from character to numeric so it could be used for statistical analysis.

camera <- camera %>% mutate(county=recode(county,
                                          "K"="Kings County",
                                          "BK"="Kings County",
                                          "Kings"="Kings County",
                                          "Kings Count"="Kings County",
                                          "Bronx"="Kings County",
                                          "Q"="Queens County",
                                          "QN"="Queens County",
                                          "Qns"="Queens County",
                                          "BX"="Bronx County",
                                          "NY"="New York County",
                                          "MN"="New York County",
                                          "R"="Richmond County",
                                          "RICH"="Richmond County",
                                          "ST"="Richmond County"))

We also recoded county abbreviations into their full county names to improve clarity and consistency.

2.5 Payment Amount by Agency

2.5.1 Visualization

ggplot(camera, aes(x = issuing_agency, y = payment_amount)) +
  geom_boxplot() +
  theme_minimal() +
  coord_flip() +
  labs(
    title = "Payment Amount by Agency",
    x = "Agency",
    y = "Payment Amount ($)"
  )

## Warning: Removed 65 rows containing non-finite outside the scale range
## (`stat_boxplot()`).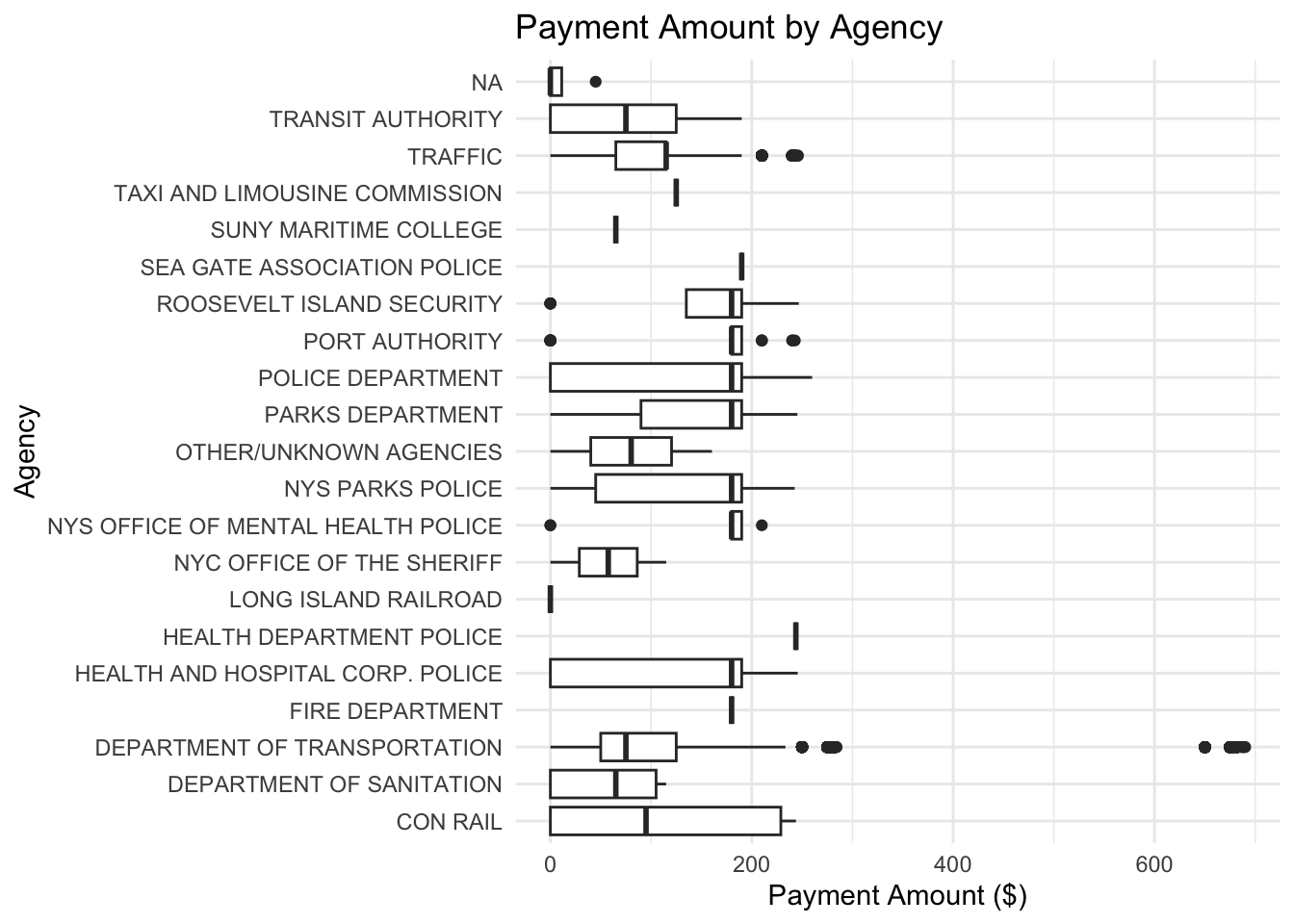

Figure 2.1: Boxplot showing the distribution of payment amounts across issuing agencies. This figure highlights differences in typical payment amounts and variability between agencies.

2.5.2 Descriptive Statistics

favstats(payment_amount ~ issuing_agency, data = camera) %>% arrange(desc(mean))

##                        issuing_agency    min      Q1 median       Q3    max      mean
## 1            HEALTH DEPARTMENT POLICE 243.81 243.810 243.81 243.8100 243.81 243.81000
## 2         SEA GATE ASSOCIATION POLICE 190.00 190.000 190.00 190.0000 190.00 190.00000
## 3                     FIRE DEPARTMENT 180.00 180.000 180.00 180.0000 180.00 180.00000
## 4  NYS OFFICE OF MENTAL HEALTH POLICE   0.00 180.000 180.00 190.0000 210.00 161.33333
## 5           ROOSEVELT ISLAND SECURITY   0.00 135.000 180.00 190.0000 246.68 149.16083
## 6                      PORT AUTHORITY   0.00 180.000 180.00 190.0000 242.76 147.35792
## 7                    NYS PARKS POLICE   0.00  45.000 180.00 190.0000 242.58 143.86176
## 8                    PARKS DEPARTMENT   0.00  90.000 180.00 190.0000 245.28 128.47736
## 9       TAXI AND LIMOUSINE COMMISSION 125.00 125.000 125.00 125.0000 125.00 125.00000
## 10   HEALTH AND HOSPITAL CORP. POLICE   0.00   0.000 180.00 190.0000 245.64 124.71373
## 11                  POLICE DEPARTMENT   0.00   0.000 180.00 190.0000 260.00 123.93855
## 12                           CON RAIL   0.00   0.000  95.00 228.8875 243.87 112.62000
## 13       DEPARTMENT OF TRANSPORTATION   0.00  50.000  75.00 125.0000 690.04  99.52822
## 14                            TRAFFIC   0.00  65.000 115.00 115.0000 245.79  94.59362
## 15             OTHER/UNKNOWN AGENCIES   0.00  40.115  80.23 120.3450 160.46  80.23000
## 16                  TRANSIT AUTHORITY   0.00   0.000  75.00 125.0000 190.00  78.00000
## 17              SUNY MARITIME COLLEGE  65.00  65.000  65.00  65.0000  65.00  65.00000
## 18          NYC OFFICE OF THE SHERIFF   0.00  28.750  57.50  86.2500 115.00  57.50000
## 19           DEPARTMENT OF SANITATION   0.00   0.000  65.00 105.0000 115.00  56.78571
## 20               LONG ISLAND RAILROAD   0.00   0.000   0.00   0.0000   0.00   0.00000
##           sd     n missing
## 1         NA     1       0
## 2    0.00000     2       0
## 3         NA     1       0
## 4   65.99423    15       0
## 5   90.57967    24       0
## 6   82.58394    48       0
## 7   89.24158    34       0
## 8   78.92728   144       0
## 9         NA     1       0
## 10  98.60130    51       0
## 11  88.00388   214       0
## 12 124.87146     6       0
## 13  82.88394 87273       0
## 14  44.47453 12091       0
## 15 113.46235     2       0
## 16  82.05181     5       0
## 17        NA     1       0
## 18  81.31728     2       0
## 19  48.26239    14       0
## 20        NA     1       0

2.5.3 Inferential Statistics

anova_agency <- aov(payment_amount ~ issuing_agency, data = camera)
summary(anova_agency)

##                   Df    Sum Sq Mean Sq F value Pr(>F)    
## issuing_agency    19    937675   49351   7.858 <2e-16 ***
## Residuals      99910 627464684    6280                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 69 observations deleted due to missingness

supernova(anova_agency)

## Refitting to remove 69 cases with missing value(s)
## ℹ aov(formula = payment_amount ~ issuing_agency, data = listwise_delete(camera, 
##     c("payment_amount", "issuing_agency")))

##  Analysis of Variance Table (Type III SS)
##  Model: payment_amount ~ issuing_agency
## 
##                                     SS    df        MS     F   PRE     p
##  ----- --------------- | ------------- ----- --------- ----- ----- -----
##  Model (error reduced) |    937675.432    19 49351.339 7.858 .0015 .0000
##  Error (from model)    | 627464683.951 99910  6280.299                  
##  ----- --------------- | ------------- ----- --------- ----- ----- -----
##  Total (empty model)   | 628402359.383 99929  6288.488

The ANOVA results show that the Sum of Squares for issuing_agency (SS = 937,675) is much smaller than the Residuals (SS = 6,274,646,484), meaning agency explains very little of the variance in payment_amount. The F value of 7.86 and very low p-value (< .001) show a statistically significant difference between agencies, but the PRE value (0.0015) indicates that agency explains only about 0.15% of the variance. In other words, the result is statistically significant but too small to matter in real-world terms.

2.5.4 Interpretation

The results show that while there are some differences in payment amounts between agencies, the difference is very small. Even though the test came out statistically significant, the actual effect isn’t meaningful in the real world. This means that the type of agency doesn’t really change how much people end up paying. So, I would not recommend the law firm focus on agency as part of their marketing strategy since it doesn’t seem to have a big impact.

2.6 Payment Amount by Tri-State (NY, NJ, CT)

2.6.1 Visualization

camera_tri <- camera %>% filter(state %in% c("NY","NJ","CT"))

#plate_state x payment_amount
ggplot(camera_tri, aes(x = state, y = payment_amount)) +
  geom_boxplot() +
  theme_minimal() +
  coord_flip() +
  labs(
    title = "Payment Amount by State",
    x = "State",
    y = "Payment Amount ($)"
  )

## Warning: Removed 15 rows containing non-finite outside the scale range
## (`stat_boxplot()`).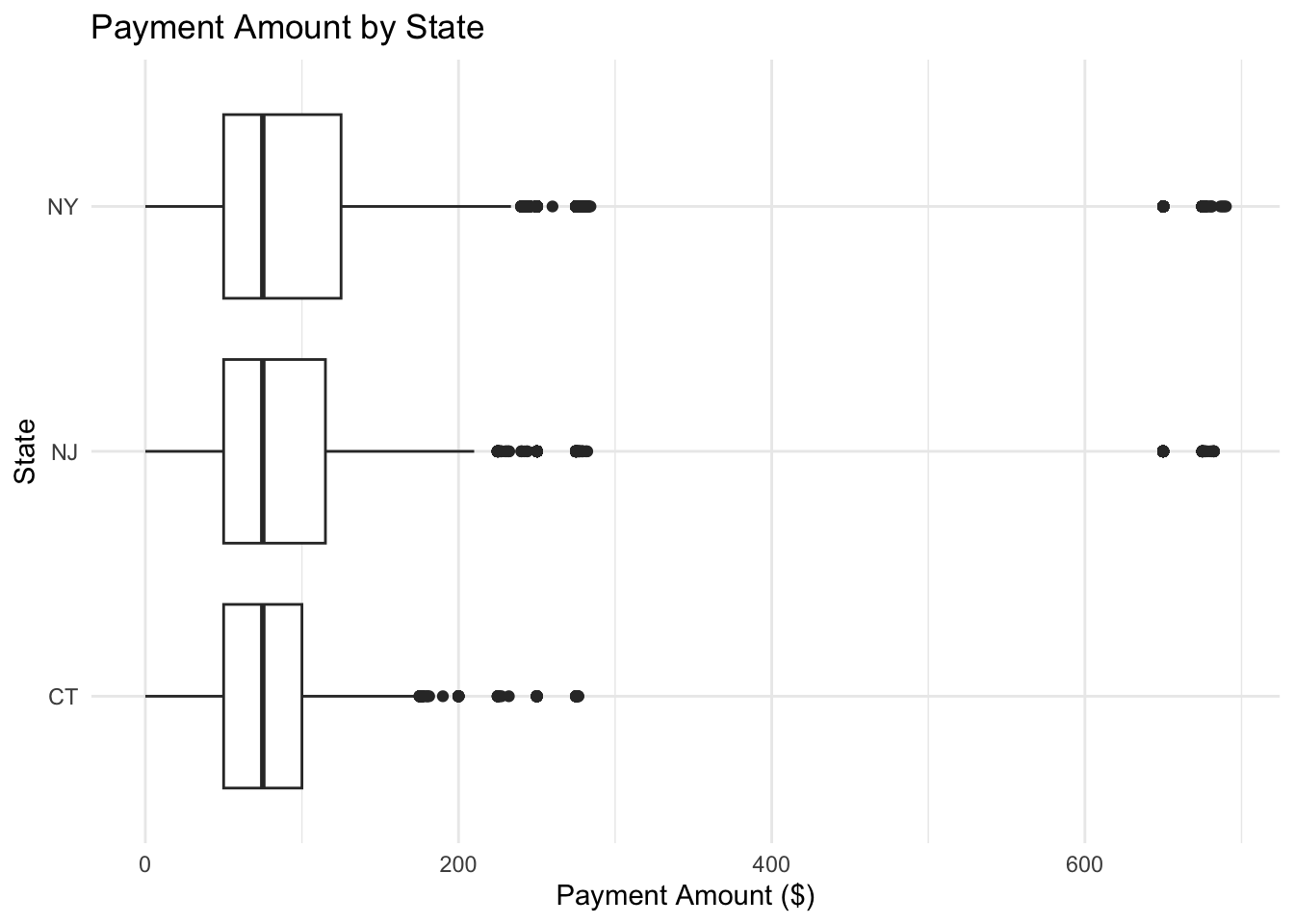

Figure 2.2: Boxplot showing the distribution of payment amounts for vehicles registered in New York (NY), New Jersey (NJ), and Connecticut (CT). This figure compares typical payment amounts and variability across neighboring states.

2.6.2 Descriptive Statistics

favstats(payment_amount ~ state, data = camera_tri) %>% arrange(desc(mean))

##   state min Q1 median  Q3    max     mean       sd     n missing
## 1    NJ   0 50     75 115 682.35 101.5746 89.97170  8654       3
## 2    NY   0 50     75 125 690.04 101.0902 80.93015 79541      10
## 3    CT   0 50     75 100 276.57  80.6627 46.07849  1457       2

2.6.3 Inferential Statistics

anova_state <- aov(payment_amount ~ state, data = camera_tri)
summary(anova_state)

##                Df    Sum Sq Mean Sq F value Pr(>F)    
## state           2    602716  301358   45.48 <2e-16 ***
## Residuals   89649 594098897    6627                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 15 observations deleted due to missingness

supernova(anova_state)

## Refitting to remove 15 cases with missing value(s)
## ℹ aov(formula = payment_amount ~ state, data = listwise_delete(camera_tri, 
##     c("payment_amount", "state")))

##  Analysis of Variance Table (Type III SS)
##  Model: payment_amount ~ state
## 
##                                     SS    df         MS      F   PRE     p
##  ----- --------------- | ------------- ----- ---------- ------ ----- -----
##  Model (error reduced) |    602716.142     2 301358.071 45.475 .0010 .0000
##  Error (from model)    | 594098896.889 89649   6626.944                   
##  ----- --------------- | ------------- ----- ---------- ------ ----- -----
##  Total (empty model)   | 594701613.031 89651   6633.519

The ANOVA results show that the Sum of Squares for state (SS = 602,716) is much smaller than the Residuals (SS = 59,409,889,897), meaning that state accounts for only a very small amount of variation in payment_amount. The F value of 45.48 and low p-value (< .001) indicate a statistically significant difference in payment amounts between states, but the PRE value (0.001) shows that state explains only about 0.1% of the variance. This suggests that while there is a statistical difference across NY, NJ, and CT, the effect is minimal and not practically meaningful.

2.6.4 Interpretation

The results show that there are some differences in payment amounts between New York, New Jersey, and Connecticut, but the differences are very small. Even though the test came out statistically significant, it doesn’t make a real impact in the real world. The state someone is from doesn’t seem to strongly affect how much they pay for their tickets. As a result, I would not recommend the law firm use state as a focus in their marketing strategy since it doesn’t seem to be an important factor.

2.7 Payment Amount by County

2.7.1 Visualization

ggplot(camera, aes(x = county, y = payment_amount)) +
  geom_boxplot() +
  theme_minimal() +
  coord_flip() +
  labs(
    title = "Payment Amount by County",
    x = "County",
    y = "Payment Amount ($)"
  )

## Warning: Removed 65 rows containing non-finite outside the scale range
## (`stat_boxplot()`).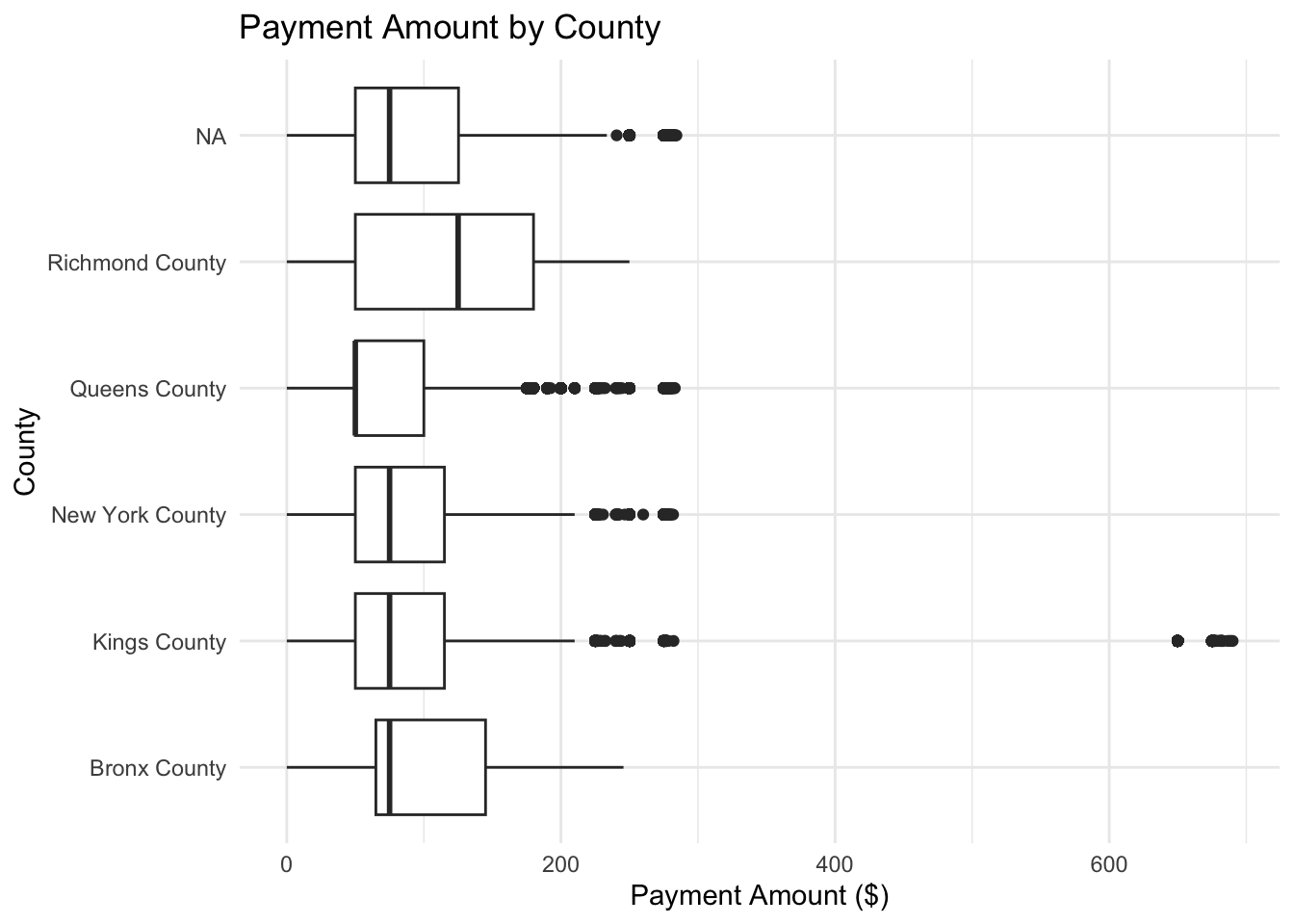

Figure 2.3: Boxplot showing the distribution of payment amounts across counties. This figure compares typical payment amounts and variability between counties.

2.7.2 Descriptive Statistics

favstats(payment_amount ~ county, data = camera) %>% arrange(desc(mean))

##            county min Q1 median  Q3    max      mean        sd     n missing
## 1 Richmond County   0 50    125 180 250.00 114.53669  77.55385  1349       0
## 2    Kings County   0 50     75 115 690.04 110.89009 126.20057 16113       0
## 3    Bronx County   0 65     75 145 245.64  99.59634  67.66429   246       0
## 4 New York County   0 50     75 115 281.80  97.62502  62.55866 23479       0
## 5   Queens County   0 50     50 100 283.03  83.46501  60.08515 17366       0

2.7.3 Inferential Statistics

anova_county <- aov(payment_amount ~ county, data = camera)
summary(anova_county)

##                Df    Sum Sq Mean Sq F value Pr(>F)    
## county          4   6702697 1675674   233.4 <2e-16 ***
## Residuals   58548 420413252    7181                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 41446 observations deleted due to missingness

supernova(anova_county)

## Refitting to remove 41446 cases with missing value(s)
## ℹ aov(formula = payment_amount ~ county, data = listwise_delete(camera, 
##     c("payment_amount", "county")))

##  Analysis of Variance Table (Type III SS)
##  Model: payment_amount ~ county
## 
##                                     SS    df          MS       F   PRE     p
##  ----- --------------- | ------------- ----- ----------- ------- ----- -----
##  Model (error reduced) |   6702697.176     4 1675674.294 233.359 .0157 .0000
##  Error (from model)    | 420413251.683 58548    7180.659                    
##  ----- --------------- | ------------- ----- ----------- ------- ----- -----
##  Total (empty model)   | 427115948.859 58552    7294.643

The ANOVA results show that the Sum of Squares for county (SS = 6,702,697) is small compared to the Residuals (SS = 42,041,325,252), meaning that county explains only a small amount of the total variance in payment_amount. The Mean Square for county is higher than the residual Mean Square, showing that there are some differences in payment amounts between counties. The F value of 233.36 is quite large, and the very small p-value (< .001) shows that these differences are statistically significant. However, the PRE value of 0.0157 indicates that only about 1.57% of the total variance in payment_amount is explained by county. This means that while the result is statistically significant, the actual differences in payment amounts between counties are still very small and not practical.

2.7.4 Interpretation

Again, the results show that while payment amounts vary slightly across different counties, the differences are very small overall. Even though the analysis was statistically significant, it doesn’t make a real-world impact. This suggests that the county where a ticket is issued doesn’t strongly affect how much people pay. Therefore, I would not recommend the law firm focus on county differences in their marketing strategy either, since it’s not an important factor influencing payment amounts.

2.8 Concluding Summary

After comparing payment amounts by agency, state, and county, none of the variables really stood out as being meaningful in explaining differences in payment amounts. While all three tests were statistically significant, the actual differences were very small in real-world terms. This means that factors like agency type, state, or county don’t seem to strongly influence how much people pay for their tickets. For that reason, I wouldn’t recommend the firm focus on any of these variables for marketing purposes. Instead, it may be more useful to explore other factors, like the type of vehicle, which might be a better predictor of higher payments.